Точки перелома функции это

Определения и классификация точек разрыва функции

Определение точки разрыва функции

Конечная точка x0 называется точкой разрыва функции f(x), если функция определена на некоторой проколотой окрестности точки x0, но не является непрерывной в этой точке.

То есть, в точке разрыва, функция либо не определена, либо определена, но хотя бы один односторонний предел в этой точке или не существует, или не равен значению f(x0) функции в точке x0. См. «Определение непрерывности функции в точке».

Определение точки разрыва 1-го рода

Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :

.

Определение скачка функции

Скачком Δ функции в точке называется разность пределов справа и слева

.

Определение точки устранимого разрыва

Точка называется точкой устранимого разрыва, если существует предел

,

но функция в точке или не определена, или не равна предельному значению: .

Таким образом, точка устранимого разрыва – это точка разрыва первого рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода

Точка разрыва называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Исследование функций на непрерывность

При исследовании функций на непрерывность мы используем следующие факты.

• Элементарные функции и обратные к ним непрерывны на своей области определения. К ним относятся следующие функции:

  , а также постоянная и обратные к ним функции. См. «Справочник по элементарным функциям».

• Сумма, разность и произведение непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве.

  Частное двух непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве, за исключением точек, в которых знаменатель дроби обращается в нуль. См. «Арифметические свойства непрерывных функций»

• Сложная функция непрерывна в точке , если функция непрерывна в точке , а функция непрерывна в точке . См. «Предел и непрерывность сложной функции»

Примеры

Все примеры Далее мы приводим подробные решения примеров, в которых требуется исследовать функцию на непрерывность и установить вид точек разрыва, если есть.

в точках ⇓;

⇓; ⇓.

Пример 1

Все примеры ⇑ Задана функция и два значения аргумента и . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.

.

Решение

Заданная функция является сложной. Ее можно рассматривать как композицию двух функций:

, . Тогда

.

Рассмотрим функцию . Она составлена из функции и постоянных с помощью арифметических операций сложения и деления. Функция является элементарной – степенной функцией с показателем степени 1. Она определена и непрерывна для всех значений переменной . Поэтому функция определена и непрерывна для всех , кроме точек, в которых знаменатель дроби обращается в нуль. Приравниваем знаменатель к нулю и решаем уравнение:

.

Получаем единственный корень .

Итак, функция определена и непрерывна для всех , кроме точки .

Рассмотрим функцию . Это показательная функция с положительным основанием степени. Она определена и непрерывна для всех значений переменной .

Поэтому заданная функция определена и непрерывна для всех значений переменной , кроме точки .

Таким образом, в точке , заданная функция является непрерывной.

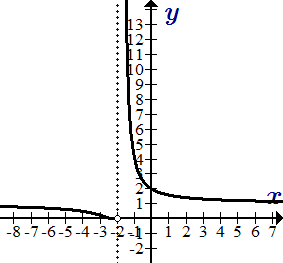
График функции y = 41/(x+2).

Рассмотрим точку . В этой точке функция не определена. Поэтому она не является непрерывной. Установим род разрыва. Для этого находим односторонние пределы.

Используя связь между бесконечно большими и бесконечно малыми функциями, для предела слева имеем:

при ,

,

,

.

Здесь мы использовали следующие общепринятые обозначения:

.

Также мы использовали свойство показательной функции с основанием :

.

Аналогично, для предела справа имеем:

при ,

,

,

.

Поскольку один из односторонних пределов равен бесконечности, то в точке разрыв второго рода.

Ответ

В точке функция непрерывна.

В точке разрыв второго рода,

.

Пример 2

Все примеры ⇑ Задана функция . Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.

.

Решение

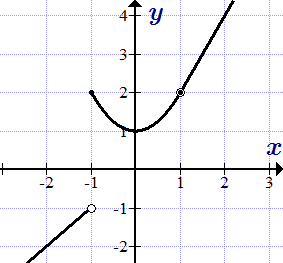
График заданной функции.

Функция является степенной функцией с целым показателем степени, равным 1. Такую функцию также называют линейной. Она определена и непрерывна для всех значений переменной .

В входят еще две функции: и . Они составлены из функции и постоянных с помощью арифметических операций сложения и умножения:

, .

Поэтому они также непрерывны для всех .

Поскольку функции, входящие в состав непрерывны для всех , то может иметь точки разрыва только в точках склейки ее составляющих. Это точки и . Исследуем на непрерывность в этих точках. Для этого найдем односторонние пределы.

Рассмотрим точку . Чтобы найти левый предел функции в этой точке, мы должны использовать значения этой функции в любой левой проколотой окрестности точки . Возьмем окрестность . На ней . Тогда предел слева:

.

Здесь мы использовали тот факт, что функция является непрерывной в точке (как и в любой другой точке). Поэтому ее левый (как и правый) предел равен значению функции в этой точке.

Найдем правый предел в точке . Для этого мы должны использовать значения функции в любой правой проколотой окрестности этой точки. Возьмем окрестность . На ней . Тогда предел справа:

.

Здесь мы также воспользовались непрерывностью функции .

Поскольку, в точке , предел слева не равен пределу справа, то в ней функция не является непрерывной – это точка разрыва. Поскольку односторонние пределы конечны, то это точка разрыва первого рода. Скачек функции:

.

Теперь рассмотрим точку . Тем же способом вычисляем односторонние пределы:

;

.

Поскольку функция определена в точке и левый предел равен правому, то функция непрерывна в этой точке.

Ответ

Функция имеет разрыв первого рода в точке . Скачек функции в ней: . В остальных точках функция непрерывна.

Пример 3

Все примеры ⇑ Определить точки разрыва функции и исследовать характер этих точек, если

.

Решение

Воспользуемся тем, что линейная функция определена и непрерывна для всех . Заданная функция составлена из линейной функции и постоянных с помощью арифметических операций сложения, вычитания, умножения и деления:

.

Поэтому она определена и непрерывна для всех , за исключением точек, в которых знаменатель дроби обращается в нуль.

Найдем эти точки. Приравниваем знаменатель к нулю и решаем квадратное уравнение:

;

;

; .

Тогда

.

Используем формулу:

.

С ее помощью, разложим числитель на множители:

.

Тогда заданная функция примет вид:

(П1) .

Она определена и непрерывна для всех , кроме точек и . Поэтому точки и являются точками разрыва функции.

Разделим числитель и знаменатель дроби в (П1) на :

(П2) .

Такую операцию мы можем проделать, если . Таким образом,

при .

То есть функции и отличаются только в одной точке: определена при , а в этой точке не определена.

Чтобы определить род точек разрыва, нам нужно найти односторонние пределы функции в точках и . Для их вычисления мы воспользуемся тем, что если значения функции изменить, или сделать неопределенными в конечном числе точек, то это не окажет ни какого влияние на величину или существование предела в произвольной точке (см. «Влияние значений функции в конечном числе точек на величину предела»). То есть пределы функции в любых точках равны пределам функции .

Рассмотрим точку . Знаменатель дроби в функции , при в нуль не обращается. Поэтому она определена и непрерывна при . Отсюда следует, что существует предел при и он равен значению функции в этой точке:

.

Поэтому точка является точкой устранимого разрыва первого рода.

Рассмотрим точку . Используя связь бесконечно малых и бесконечно больших функций, имеем:

;

.

Поскольку пределы бесконечные, то в этой точке разрыв второго рода.

Ответ

Функция имеет точку устранимого разрыва первого рода при , и точку разрыва второго рода при .

Использованная литература:

О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.

Автор: Олег Одинцов. Опубликовано: 22-09-2018

Источник

Источник

Функция f(x) называется непрерывной в точке х = а если:

1) она определена в этой точке;

2) существует предел функции в этой точке

3) значение предела равно значению функции в точке х = а, т.е.

Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.

Классификация точек разрыва

Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа

и слева

.

Если, кроме этого, выполняется хотя бы одно из условий

то функция в точке х = а имеет неустранимый разрыв первого рода.

Если пределы равны, однако функция не существует

то имеем устранимый разрыв первого рода.

Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа или слева не существует или бесконечна.

Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ

если они разные и не равны бесконечности.

При нахождении точек разрыва функции можно руководствоваться следующими правилами:

1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале.

2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки.

3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.

Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.

Рассмотрим несколько задач по данной теме.

Задача 1.

Найти точки разрыва функции

а)

Решение:

Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая

Найдем односторонние пределы в точках разрыва

При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.

Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы являются точками разрыва второго рода. График функции приведен на рисунке ниже

——————————————————-

б)

Решение:

Задача достаточно простая. В первую очередь находим нули знаменателя

Таким образом функция определена на всей действительной оси за исключением точек , которые являются точками разрыва. Вычислим односторонние пределы справа и слева

Пределы бесконечны поэтому, по определению, имеем точки разрыва второго рода.

Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.

——————————————————-

в)

Решение:

Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке

Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.

——————————————————-

Задача 2.

Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.

а)

Решение:

Для заданной функции точка x = 2 является точкой разрыва. Найдем предел функции , чтобы определить характер разрыва

По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2

График функции на интервале который нас интересует приведен далее

——————————————————-

б)

Решение:

Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы

Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция – непрерывная.

Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.

Исследуем на непрерывность вторую точку

По определению функция в точке x = 2 имеет неустранимый разрыв І рода.

Прыжок функции равен 29 – (- 3) = 31.

По условию задания построим график функции.

Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.

Источник