Перелом эпюры

ЭПЮРЫ ИЗГИБАЮЩЕГО МОМЕНТА (продолжение)
В продолжение темы и лучшего усвоения материала предложим Вам следующие примеры.
Балка, опертая по концам (рис.2), но сила внешнего воздействия сместилась к одному из концов балки. Из пройденного материала известно, что при простом изгибе балки, опертой по концам, при изгибе ее под воздействием сосредоточенной силы, эпюры максимальных сжимающих и растягивающих напряжений симметричны (ось симметрии проходит через точки опирания балки, то есть через балку до ее деформации) (рис.1).
Рис.1. Опертая по концам балка, симметричное нагружение
Поэтому, чтобы не загружать схему, рассмотрим только эпюру растягивающих напряжений. Строим эпюру максимальных растягивающих напряжений, реализующихся по длине балки: проецируем «главные действующие лица» (точки опоры и место приложения силы) на горизонтальную ось, от точки проекции силы откладываем ее значение (длину) по вертикали и соединяем полученные три точки…(рис.2).
Рис. 2. Построение эпюры максимальных растягивающих напряжений (балка, опертая по концам, несимметричное нагружение)
Непонятно? Предлагаю использовать способ построения эпюры при помощи резинки… Крепим резинку к двум точкам опоры и давим на нее пальцем (рис.3). Получаем эпюру максимального растягивающего напряжения по длиннику балки (самое интересное, что данный способ математически верен)!
Рис.3
До этого мы рассматривали, как выглядят максимальные эпюры сжатия и растяжения вдоль оси рассматриваемой балки. Как выглядят эпюры сжатия и растяжения в перпендикулярном сечении, то есть, как выглядит топография напряжений сжатия и растяжения в поперечнике балки (сверху вниз)?
Увеличим балку до цилиндра, переведя ее из схемы в «реальный» объект (рис. 4, б). По нижнему краю цилиндра при изгибе формируются растягивающие напряжения (схема на рис. 4, а), по верхнему краю (из пройденного материала) – сжимающие напряжения. Чтобы сформировалось сжатие, напряжения должны быть направлены к середине балки, а что бы сформировалось растяжение – напряжения должны быть направлены за пределы балки.
Рис.4. Балка, опертая по концам, несимметричное нагружение
Почему вектора напряжений (стрелки красного и синего цвета) на рисунке «4 в» только с одного конца цилиндра – спросите Вы? Все верно, с другого конца цилиндра можно расположить аналогичные стрелки красного и синего цвета, симметрично (относительно вертикальной оси) направив красные кнутри, а синие (растягивающие) кнаружи (см. рис.4 б). Однако, вспомнив ранее изложенный материал на простое растяжение и сжатие, вы легко поймете, что достаточно одной пары групп стрелок. В зоне направления красных стрелок (векторов) на всем протяжении будет реализовываться сжатие, а в зоне синих – растяжение.
Внимательный читатель давно обратил внимание, что вектора напряжений, как сжимающих, так и растягивающих, имеют наибольшую величину по верхнему и нижнему (соответственно) краям цилиндра, а ближе к центру происходит их уменьшение. Нулевая точка соответствует оси симметрии балки. Действительно, при деформациях внутренние слои испытывают минимальные напряжения и деформации.
Этой особенностью концентрации напряжений активно и умело пользуется природа, обеспечивая минимальный вес конструкции при максимальной прочности. Зачем делать из прочного материала внутренние слои какой-либо конструкции, если эти слои не подвергаются, а значит и не противостоят внешнему воздействию и деформации? Конечно, там лучше убрать материал вовсе! В результате в биологии мы получаем, например диафиз трубчатой кости, а в строительстве швеллер, двутавр и т.д.
Высота треугольника эпюры зависит от величины приложенной силы, в нашем случае, достаточно абстрактной. Тем не менее, если силу мы уменьшим в два раза, настолько же уменьшится и высота треугольника эпюры (рис.5).
Рис.5. Балка, опертая по концам, несимметричное нагружение
А что происходит в реальности? Правильны ли наши умозаключения?
Метод конечных элементов, компьютерное моделирование позволяют увидеть топографию напряжений.
Пример. Рассматривается кость, фиксированная головками к упругой подложке. По кости в средней ее части осуществляется воздействие острого индентора. На рисунке 6 приводятся результаты математического моделирования методом конечных элементов процесса разрушения кости (это один из слайдов).
Пусть Вас не пугает смена цветов (на схемах выше мы сжатие отмечали красным, а растяжение синим). Компьютерная программа (если не изменять настроек) наиболее критические состояния отмечает (а они в данном случае в зоне растяжения) оттенками красного цвета.
Рис. 6. Внедрение индентора под углом 90°. Оттенками красного отмечены растягивающие напряжения, оттенками синего – сжимающие
Как такой перелом выглядит в реальности? На рисунке 7 представлен полный поперечный (безоскольчатый) перелом большеберцовой кости. Удар нанесен по гребню большеберцовой кости сосредоточенной силой – острым индентором (средней частью лезвия топора).
Рис.7. Полный поперечный перелом большеберцовой кости (действие острого индентора)
Сосредоточенная сила… кто-то из практических экспертов скажет: «да где ее встретишь, ну тупой топор и что-нибудь подобное…ты нам бампер подавай».
Давайте попробуем разобраться в этом вопросе вместе. Представим, что наезд на пешехода произошел сзади (рис. 8).
Рис. 8. Наезд ТС на пешехода сзади
Упрощаем задачу, приняв, что силы трения и инерции тела в сравнении с импульсом удара бампера формируют прочную фиксацию обоих концов балки (ноги), но суставы обеспечивают возможность поворота как минимум в одной плоскости, а бампер автомобиля прямоугольной формы, шириной, например в зоне контакта 5-6 см.
Рассмотреть взаимодействие балки и предмета, которые имеют определенную форму и размеры достаточно сложно. В сопромате этот сложный процесс называется контактной задачей. При ее решении приходится учитывать и силы трения, и форму контактирующих поверхностей. Чтобы упростить такую сложную задачу, заменим бампер группой сил, действующими на определенном ограниченном участке (рис.9).
Рис. 9. Построение схемы нагружения
Как будет выглядеть эпюра максимальных растягивающих напряжений в этом случае? Напряжения некоторым образом суммируются, и вершина треугольника получается сглаженной (рис.10)
Рис. 10.
Непонятно? Предлагаю призвать на помощь резинку… Крепим резинку к двум точкам опоры и сыпем на нее песок (с единственным допущением, что он распределяется на строго определенном нами участке, соответствующем границам крайних сил и не пересыпается за пунктирные линии рисунка) (рис.11). Получаем эпюру максимального растягивающего напряжения по длиннику балки! (и этот способ математически верен!).
Рис.11.
Из построенных эпюр видно, что прогнозируемая зона разрыва должна реализоваться в области «сглаженной» вершины, которую мы вам дали на схеме с «увеличением» на рисунке 9.
А что же происходит на поверхности балки со стороны воздействия индентора? Эпюра напряжений в области контакта индентора и балки имеет следующий вид (рис.12):
Рис. 12
Верны ли наши рассуждения? Сравним наши данные с данными моделирования процесса нагружения балки тупым (прямоугольным) индентором. На рисунке 13 наглядно демонстрируются поля напряжений, как в зоне растяжения, так и в зоне сжатия (использованная программная среда не отличает растяжение и сжатия; синим цветом и его оттенками отмечены зоны «спокойствия», а оттенками красного – «критические» участки). Для наглядности к картине полей напряжений мы «прикрепили» индентор и точки опирания.
Рис.13
Теперь рассмотрим процесс формирования перелома. В зоне наибольшего растяжения, где-то в области сглаженной вершины, построенной нами, появляются микроразрушения (рис.14,а). Микроскопические разрушения объединяются, и формируется разрыв. Зарождение и разрыв… полукруглая блестящая мелкозернистая поверхность с отвесными краями дает развитие магистральной трещине, появляются касательные напряжения (к ним мы обратимся обязательно, но чуть позже), направленные под углом 45° к нормали. Формируется поверхность излома, на которой регистрируются рубцы в виде шевронов, елочки и т.д. … Куда идти трещине? (на рисунке 14,б мы ее отметили зеленым цветом).
Рис.14.
Ровно посредине кости зона растяжения сменяется зоной сжатия (см. рис.3 – эпюра в виде «двух треугольников»). На рисунке 1, и, соответственно в первом абзаце, мы приняли как аксиому, что эпюры максимальных сжимающих и растягивающих напряжений симметричны. Поэтому эпюра максимального сжимающего напряжения аналогична эпюре растягивающего напряжения и имеет форму в виде треугольника со скругленной вершиной (рис.15).
Рис.15.
Трещина, определяясь с направлением развития, решает проблему самым энергетически выгодным способом – идет по пути наименьших затрат.
Движение по пути наименьшего сопротивления. Направление наименьшего сопротивления соответствует точкам опоры (поскольку на всем пути напряжения растягивающие, зоны сжатия, которые необходимо преодолевать, не встречаются), но расстояние при этом, которое предстоит преодолеть трещине, наибольшее (рис.16).
Рис.16.
Движение по наикратчайшему пути. Самое короткое расстояние для пересечения толщи кости – это путь от зоны разрыва к точке контакта с индентором (рис.17). Но здесь располагается зона наибольшего сжатия (то же не выгодно). Выход простой – эту зону надо обойти.
Рис.17.
Трещина принимает соломоново решение (между «расстоянием» и «сопротивлением»): она берет направление близкое к 45° к длиннику кости (рис.18)
Рис.18.
А как же индентор и локальное нагружение? Локальное нагружение трещина воспринимает совершенно реально и обходит его тоже (рис.19).
И если нагружение симметричное, трещина раздваивается и формирует треугольный отломок (рис.19,а), а если не симметричное – косой перелом (рис.19,б) (несимметричное нагружение может быть вызвано отклонением силы от перпендикулярной оси, изменением сечения кости, условиями опирания, всем тем, чего в биосистемах больше, чем достаточно).
Рис.19.
В итоге, получаем перелом (рис.20), подобный изображенному на рисунке 19,а.
Рис. 20.
Источник
Эпюрами называют геометрические образы, применяемые для изображения изменения в элементе какого-либо силового фактора либо иных данных.
Примеры построения эпюр
Эпюры внутренних усилий (поперечных сил и изгибающих моментов) для простейших систем показаны на рисунке 3.1.
Рисунок 3.1 – Эпюры внутренних усилий для простейших балок
Отметим, что в строительной механике, на эпюре изгибающих моментов знак, как правило, не ставится, и в отличие от сопромата, она строится со стороны растянутых волокон.
Эпюры для однопролетных балок с консолями строят в следующем порядке:
- сначала строят эпюры на консолях, используя таблицы изгибающих моментов для консольных балок (рисунок 3.1), фиксируя при этом консольные моменты;
- отмечая опорные моменты, проводят так называемую линию опорных моментов. Это прямая, соединяющая ординаты моментов над опорами;
- на линию опорных моментов накладывают пролетную балочную эпюру (табличная эпюра М для однопролетной балки) от соответствующего вида загружения;
- все эпюры М строят со стороны растянутых волокон.
Между выражениями для изгибающего момента, поперечной силы и интенсивностью распределенной нагрузки в пределах расчетного силового участка существуют известные из курса “Сопротивление материалов” дифференциальные зависимости.
Они легко выводятся с помощью уравнений равновесия, составленных для вырезанного бесконечно малого элемента (рисунок 3.2):
Рисунок 3.2 – Определение значений поперечной силы
Внутренние силы в основных типах элементов систем:
- ферменный элемент – это стержень, имеющий по концам шарнирное (безмоментное) закрепление. В этом элементе при отсутствии собственной поперечной нагрузки возникают лишь продольные силы.
- рамный (балочный) элемент – стержень, в котором возможно возникновение всех внутренних силовых факторов (N,Q,М).
Понятие о расчетном силовом участке
Расчетным силовым участком называется участок элемента системы с постоянным законом изменения всех внутренних силовых факторов.
В расчетной практике силовые участки определяются их границами.
Граница силового участка − это место приложения какой-либо сосредоточенной нагрузки (силы или момента), начало или конец распределенной нагрузки, место изменения геометрии, механических характеристик конструкции, интенсивности распределенной нагрузки.
В курсе «Строительная механика» принята следующая последовательность определения внутренних усилий (построения эпюр).
Первоначально с помощью уравнений статики в требуемых сечениях определяются изгибающие моменты.
Далее посредством дифференциальной зависимости осуществляется переход к поперечным силам. Последние дают возможность оценить и продольные силы.
Построение эпюры моментов производится по силовым участкам. При этом за расчетный модуль принимается консольная балка (рисунок 3.3).
За начало (В) принимается тот конец силового участка, на котором все внутренние и внешние воздействия определены.
Рисунок 3.3 – Консольная балка
Они (воздействия) легко (принцип независимости действия сил) приводятся к алгебраической сумме результатов простейших воздействий.
При построении эпюр внутренних усилий в многопролетных балках, рамах и других конструкциях используются эпюры М и Q в простых однопролетных и консольных балках, которые чаще всего называют табличными эпюрами моментов и поперечных сил (рисунок 3.1).
Последовательность построения эпюр внутренних усилий М, Q, N в статически определимых системах:
1) Кинематический анализ. Напомним, что нас интересуют лишь геометрически неизменяемые системы с нулевым количеством степеней свободы и правильной расстановкой связей.
2) Определение опорных реакций и реакций связи. При этом используются уравнения равновесия, составленные как для всей системы в целом, так и для любого элемента или группы элементов.
3) Построение эпюры изгибающих моментов − М.
По эпюре изгибающих моментов с помощью дифференциальной зависимости Журавского строится эпюра поперечных сил (Q).
На участке с линейной эпюрой изгибающих моментов величина поперечной силы равна тангенсу угла наклона эпюры М.
Q = |tga| – где a угол наклона касательной на эпюре М к оси балки.
Знак Q определяется по направлению кратчайшего совмещения оси участка с эпюрой. Если оно происходит по направлению движения часовой стрелки, поперечную силу считают положительной.
Если же против часовой стрелки, то отрицательной.
При построении эпюры поперечных сил для участков с криволинейной (изменяющейся только по закону квадратной параболы) эпюрой изгибающих моментов пользуются следующей зависимостью:
Q = Qо + (Мпр – Мл)/L
где Qо − поперечная сила от внешней нагрузки, приложенной на рассматриваемый участок, определенная для балки на двух опорах пролета равного L;
Мп, Мл − алгебраические величины изгибающих моментов, соответственно на правом и левом торцах рассматриваемого участка.
Вышеуказанное выражение (3.1) легко получить самостоятельно (рисунок 3.4):
Рисунок 3.4 – Вывод выражения (3)
4) По эпюре поперечных сил строится эпюра продольных сил. При этом рассматривается равновесие всех узлов системы под действием внутренних (продольных и поперечных) и внешних (узловых) сил.
5) Проводится статическая проверка правильности построения эпюр М, Q, N.
Правила для проверки правильности построенных эпюр внутренних усилий:
а) На прямолинейном ненагруженном участке эпюра моментов прямолинейна.
б) В сечении, где приложен сосредоточенный внешний момент, эпюра получает скачок на величину этого момента (рисунок 3.5), а линии эпюры моментов примыкающие к скачку идут параллельно друг другу.
Рисунок 3.5 – Эпюра М на участке с приложенным сосредоточенным моментом
в) В точке приложения сосредоточенной внешней силы Р, перпендикулярной оси стержня, эпюра моментов имеет перелом, направленный острием в сторону действия силы (рисунок 3.6).
Изменение тангенсов углов наклона эпюры в точке ее перелома равно силе Р. На эпюре Q в этой точке – скачок на величину Р в направлении ее действия.
Рисунок 3.6 – Эпюра М на участке с приложенной сосредоточенной силой Р
г) На участке, где приложена равномерно распределенная нагрузка, эпюра моментов очерчена по параболе второй степени с выпуклостью в сторону действия нагрузки и со стрелкой равной q×L2/8 (рисунок 3.7).
Рисунок 3.7 – Эпюра М на участке с равномерно распределенной нагрузкой
д) В сечениях, где нет сосредоточенной нагрузки, эпюра моментов не имеет перелома.
е) Поперечная сила в сечении стержня положительна, если она стремится вращать разделенные данным сечением части стержня по часовой стрелке (рисунок 3.8).
Рисунок 3.8 – Правило знаков для поперечной силы
Расчет внутренних усилий в рамах >
Примеры решения задач >
Источник
Эпюрами поперечных сил и изгибающих моментов называют графические изображения функций Q и M по длине балки при изгибе.
Посмотреть подробные примеры построения эпюр >>
Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.
Рассмотрим некоторые примеры на построение эпюр в балках:
Эпюры при чистом изгибе
Для консольной балки:
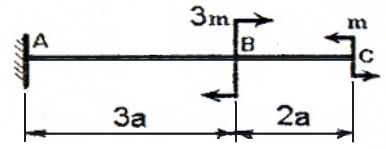
Рис. 1
имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.
Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z1 ≥ 2a (рис. 2 а,г)
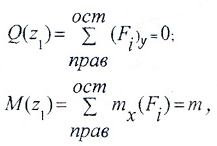
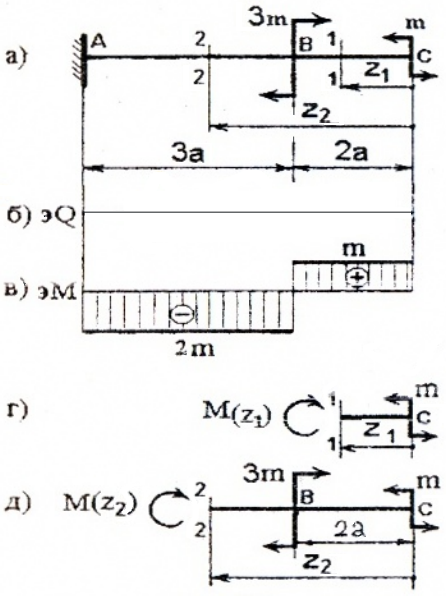
Рис. 2
т.е. Q(z1)=0 на всем участке, а M(z1)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.
II силовой участок (AB): 2a ≥ z2 ≥ 5a (рис. 2 а,д)
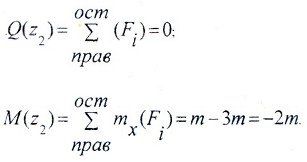
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).
Более нагруженным оказался участок AB, он и является опасным: Mmax=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.
Эпюры при поперечном изгибе
Построение эпюр Q и M для балки, изображенной на рис. 3
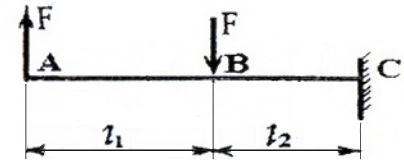
Рис. 3
проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г)
Q(z1)= F=const, на всем участке постоянная величина,
M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам:
M(z1=0)=F×0=0 – в сечении A;
M(z1=l1)=F× l1 – в сечении B.
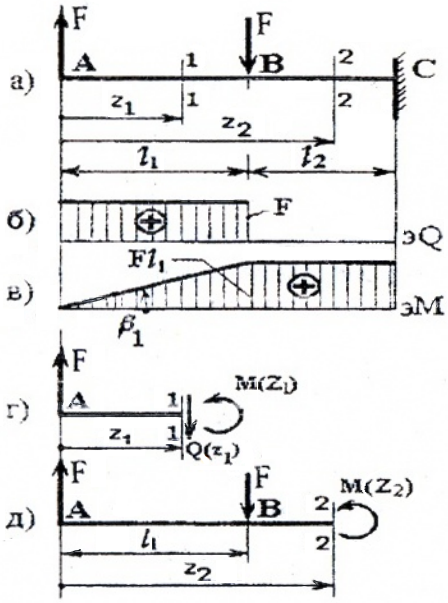
Рис. 4
II силовой участок (BC): l1 ≥ z2 ≥ (l1+ l2) (рис. 4, а, д)
Q(z2)= F-F=0;
M(z2)=F×z2- F×(z2- l1)=F ×l1=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке – деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.
Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.
Геометрическая проверка эпюр
Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим:
где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α1=0 (линия эпюры Q горизонтальна), следовательно,
распределенная нагрузка отсутствует;
функция M (z1) – возрастающая.
На участке “BC”:
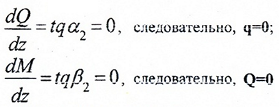
Так как все дифференциальные проверки выполняются, эпюры построены верно.
Эпюры для двухопорных балок
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),
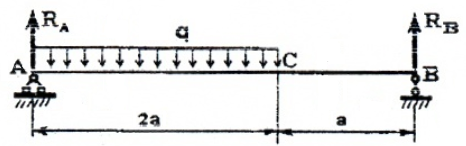
Рис. 5
необходимо вначале найти опорные реакции и только потом строить эпюры.
Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.
Записываем уравнения и находим значения реакций:
Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑FY=0 или ∑MС=0.
Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).
Для построения эпюр рассмотрим два силовых участка:
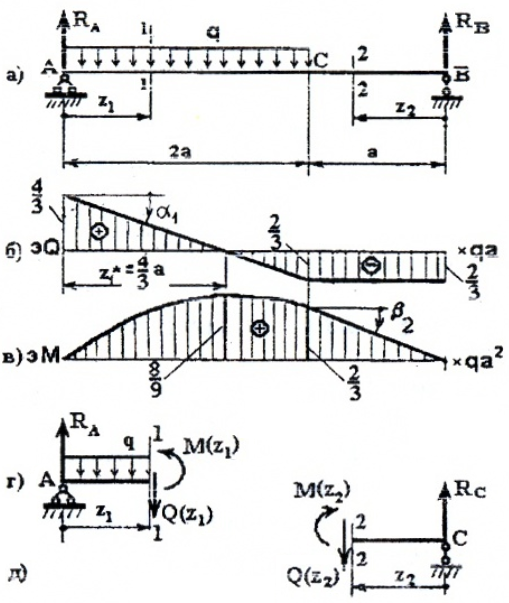
Рис. 6
I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г)
Q(z1)=RA-qz1 – прямая, которую строим по двум граничным точкам:
M(z1)=RAz1-qz1(z1/2)= RAz1-qz12/2 – парабола.
Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует Mmax(z*), и дифференциальной зависимости:
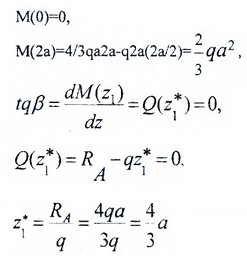
Определяем экстремум эпюры M на участке:
II участок (BC): 0 ≥ z2 ≥ a (рис. 6, а, д)
Q(z2)= -RB= -2/3qa;
M(z2)=RBz2,
M(z2=0)=0,
M(z2=a)=2/3qa2.
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z1 ≥ 2a
– направлена вниз, функция Q(z1) – убывающая.
– проверка визуально: чем больше угол наклона β1, тем больше значение Q(z1).
II силовой участок: 0 ≥ z2 ≥ a.
следовательно, q=0.
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z1*=4/3a
По силе в сечении «A»
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.
Подробные примеры построения эпюр >
Лекции по сопромату >
Примеры решения задач >
Источник
